承上篇赌徒心理系列-行为经济学,我们提到两位行为经济学代表人物,Amos Tversky和Daniel Kahneman ,两位大师根据假设来设计一些问题,给许多人来回答测试,并依据回馈来研究假设是否合理,这些设计的问题当中,很多是关于机率性质的问题,因为他们发现几乎没有人在用机率的方式在思考问题。
从近年来对于脑部科学的研究发现,我们的大脑继承了远古祖先的大脑思考方式,我们的祖先为了应付险恶的大自然生活,在演化上人类的大脑大部分是使用近乎直觉性的思考模式,所以人的大脑天生无法处理所谓的『机率』这样的一个概念,也呼应了本篇的主题,我们人类可以说是一个『机率盲』。
接下来本篇要介绍三个机率问题,分别是『三门问题』,『生日悖论』,『降雨机率』,让读者可以自己测试自己到底是不是『机率盲』。
三门问题
亦称为蒙特霍尔问题,或是蒙特霍尔悖论,他其实是个美国电视节目的游戏,游戏是这样玩的:
参赛者会看到眼前有三道关闭的门,这三道门的其中一道背后放着一台汽车,另外两道门背后则是各放一只山羊,而参赛者要打开其中一道门就可以把背后的礼物带回去(想当然每个参赛者最想带走汽车),参赛者随机选定一道门,主持人这时候还不会将门打开,反而主持人会将另外两道门的其中一道给打开,而且一定是开启有山羊的那一道门,参赛者就会看到其中一道门出现了山羊,主持人这时会问参赛者,是否要换成另一扇还未开启的门,参赛者可能就会进入考虑状态,到底是否要换呢?
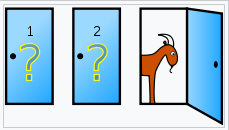
这边就衍生了一个问题,参赛者做出更换成另一道门的决定,是否会提升选到汽车的机率?
答案是:会,机率会从33%提升到66% (是否让人觉得惊讶呢?)
生日悖论
这也是一个相当有名的机率问题,问题是这样的:
一个房间要容纳几个人以上,那么在这些人当中至少能找得到其中两个人的生日同一天的机率会大于50%?
有个简易的思考方式是,一年365天,既然要大于50%,那就是365的一半,答案就是183,所以房间需要容纳183人以上,这样任意找两人是同天生日的机率才会大于50%。
上述看似正常的推理(笔者真的曾经是这样想的),但是对于熟悉机率理论的人就可看出这不是正确的计算方法与答案
正确答案是23人,很显然的比上述推论的少很多
降雨机率
若是想知道明天到底要不要带伞出门,一般来说都会查一下明天的天气预报,但是否有人曾经理解过天气预报给我们的资讯是什么?
『明天的降雨机率为70%』,这句话的意思到底是:
- 有70%的时间会下雨,另外30%不会
- 有70%的地方会下雨,另外30%不会
- 有70%的天气预报员说会下雨,另外30%说不会
- 假设通往明天的路有100条,有70条会下雨,另外30条不会
依据笔者以前考试的经验,通常答案会是最长的那个选项,没错,答案就是D选项,换种方式来说,根据机率理论的定义,D选项是相对较正确的说明方式,但是笔者在小时候真的以为答案应该是是A,B或C其中一个。
结论
本篇不打算深入讨论这几个机率问题的答案,想仔细研究的读者可以参考下列连结:
举了上面三个例子,想表达的是一般人在第一次碰上这样的问题要凭直觉找出答案是相当困难的,因为这和我们大脑的思考脉络不符,一般人也很难用『机率的思维』去思考事情,也就是大部分的人不想去思考什么叫做『70%会下雨,30%不会』,他只想知道明天到底是『会』或『不会』下雨!就如同乡民们常说的一句话,机率只有『0』或『1』,发生的时候就是1,没有发生就是0。
如果你理解大部分的人就是无法处理机率这个议题,就可以解释游戏为什么要做这么多的特效,为什么要吊玩家的胃口,以及为什么要营造看似赢钱的场景,这些效果跟机率可能没有很大的关系(但还是有点关系),必须跟玩家对于赢钱的想法有强烈的正相关才行,玩家也才愿意为你的游戏买单。
再回到赌徒的想法上,老虎机的本质就是一个机率游戏,但对于赌徒来说他看不到这一层的资讯,赌徒只想知道到底玩这个游戏到底是『会』或『不会』赢钱,而不想听到所谓的『只有10%机率会赢钱,90%会输钱』的理论说法,没办法,人就是近乎偏执的想要找到『一个答案』而已,因此厉害的老虎机设计师就会利用一些游戏特色与背后的机率,将游戏包装成让玩家玩了之后会觉得有机会赢大钱的感觉。
















暂无评论内容