本篇作為老虎機數學入門文章第一篇,要來和大家聊聊,可說是最早出現的老虎機計分規格:「Line Game」要如何計算?希望能給初次接觸的朋友清晰易懂的閱讀體驗,此篇會盡量簡單而詳盡。
早期老虎機(Stepper)
最早的老虎機相當簡單易懂,1×3的介面上,只要三格都出現一樣的圖形,就能中獎。
![图片[1]-老虎機數學入門 PART Ⅰ-学游戏](http://blog.ftuta.com/wp-content/uploads/2024/07/image.png)
我們就先從類似這樣的老虎機概念與規則來試算看看吧。
畫面:1×3 單線Bet: 1
![图片[2]-老虎機數學入門 PART Ⅰ-学游戏](http://blog.ftuta.com/wp-content/uploads/2024/07/image-1.png)
賠率表 滾輪表
![图片[3]-老虎機數學入門 PART Ⅰ-学游戏](http://blog.ftuta.com/wp-content/uploads/2024/07/e70ba-1x3%E8%B3%A0%E7%8E%87.png)
![图片[4]-老虎機數學入門 PART Ⅰ-学游戏](http://blog.ftuta.com/wp-content/uploads/2024/07/image-2.png)
先幫讀者複習一下期望值的定義:期望值 = 每次可能的結果 x 其結果出現的機率。
在這裡我們關心的是玩家拿回多少錢的期望值,所以是:所有可能的得分 x 此得分的機率。在上面規則的設置下,只要落在畫面的符號皆相同,玩家就可以獲得5倍押注得分,所以所有的得分就是:K、Q、J、10 以及9 的三連線得分總和。
先以 K 的三連線得分當例子計算:
- 第一輪有1個K
- 第二輪有1個K
- 第三輪有2個K
因此 K 三連線的組合數是 1 x 1 x 2 = 2,而三個輪子長度都是6,所以總組合數是 6 x 6 x 6 = 216。那麼就可以算出 K 三連線的機率是 2/216,RTP是 5 x 2/216 = 10/216。接著將 Q、J 、10、9 三連線得分的 RTP 也分別用一樣的方法算出並相加,就是這個設定的遊戲總 RTP 。
熱身到這裡,讀者心裡應該對算法的架構有雛型了,那麼接下來,我們就來算算建立在現代常見老虎機規格下的遊戲吧!
現代老虎機(Video Slot)
隨著科技發展,從原先的實體滾輪,發展成數位化,計分的方式也變得更多元,現在常看到的Line Game可參考下圖:
Double U《the Legend of Z》
![图片[5]-老虎機數學入門 PART Ⅰ-学游戏](http://blog.ftuta.com/wp-content/uploads/2024/07/image-3.png)
這是一個 3×5,共 25 線的 Line Game,遊戲規則已經從一開始的落在一條線上計分,變成落在遊戲設定的25條線上都有計分,並且根據三、四和五連線有不同賠率,乍看之下得分線跑得密密麻麻,似乎很複雜,但其實將他的規則拆解後,並不難理解,接下來就來和大家分享這種多線 Line Game 的計算。
遊戲規則設定
- 視窗大小:3 x 5
- 押線數:25 線 (1)
- BET:25
- 獎勵規則:
K、Q、J、10、9:出現在所有轉輪,相同符號由左至右連線時依賠率表得到獎勵。(2)
SCATTER:以在視窗出現的個數依賠率表得到獎勵。(3)
WILD(WW):可以取代除了 SCATTER 外的所有轉輪,出現在2、3、4 以及 5 轉輪。(4)
- 獎勵規則:
- 轉輪表與賠率表:
![图片[6]-老虎機數學入門 PART Ⅰ-学游戏](http://blog.ftuta.com/wp-content/uploads/2024/07/image-4.png)
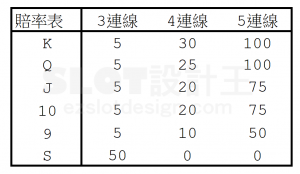
![图片[8]-老虎機數學入門 PART Ⅰ-学游戏](http://blog.ftuta.com/wp-content/uploads/2024/07/d82c2-%E8%B3%A0%E7%8E%87%E8%A1%A8_%E7%BB%93%E6%9E%9C-300x174.png)
(1) 25 線:
雖然計算的線數從1線變成25線,由於遊戲的方法多是選線押注,也就是你可以自己選擇要不要買那條線,買了才會付那條線的BET,當符號落在那條線上時才會依BET獲得相應的倍數,如果選擇不押則那條線,符號落在那條線上也不會有賠分,每條線的 RTP 除了某些特殊規則是相同且獨立的,所以多線的算法除了某些特殊的規則外,和算單線一樣。
(2) 3 連線、4 連線、5 連線:
和 1 x 3 介面不同,3 x 5 的介面多了許多得分的組合,
- 5連線仍然是符號從滾輪1到滾輪5都須出現相同符號
- 4連線是符號從滾輪1到滾輪4都須出現同樣符號,並且滾輪 5 上不能出現該符號
- 3連線要特別注意的是很容易想成符號在滾輪1~3出現並且在4、5 不出現,可是這樣會忽略掉 { K,K,K,9,K } 這類組合,所以三連線的計算會是 前三轉輪出現相同符號的組合數 x 第四轉輪不出現數 x 第五轉輪全部可能。
(3)SCATTER:
通常不要求在線上,畫面出現即可,有些規則下甚至可以不用由左至右的輪子連續出現,依遊戲規則而定,所以計算時轉輪裡一個SCATTER有三次的機會(滾輪有三格) 落在畫面上,計算時會將數量 x 3。
(4)WILD:
也會依遊戲規則有變化,有些可以替代SCATTER、有些會出現在第一滾輪,計算時要注意的是,由於 WILD 可以代替符號,在計算轉輪裡的符號時,如果該符號是能被WILD替代的,必須把WILD的數量也計入,像{K,K,W,K,K}和{K,K,K,K,K}一樣都是K五連。
遊戲計算
解釋完一些要注意的地方後,先放上完整的計算內容:(點圖可放大顯示)
![图片[9]-老虎機數學入門 PART Ⅰ-学游戏](http://blog.ftuta.com/wp-content/uploads/2024/07/image-5-1024x501.png)
我們把一些內容拉出來細看:
- 統計每個轉輪的符號數(點圖可放大顯示)
![图片[10]-老虎機數學入門 PART Ⅰ-学游戏](http://blog.ftuta.com/wp-content/uploads/2024/07/image-6-1024x779.png)
這裡處理的便是計算各個得分組合所需的、每個轉輪上統計的符號個數,會用到 <COUNTIF> 這個公式來幫助統計,
- 《 – 》是每個轉輪的符號總數,可以用公式 <SUM> ,
- 《X_》是轉輪總符號數扣掉WILD+符號的數量。
- 《3*S》注意前面也提過 SCATTER由於計算規則的關係,數量要 x 3
2.計算每種得分可能的組合數(點圖可放大顯示)
![图片[11]-老虎機數學入門 PART Ⅰ-学游戏](http://blog.ftuta.com/wp-content/uploads/2024/07/image-7-1024x569.png)
這裡會用到 <VLOOKUP> 、<PRODUCT> 來幫助計算,尤其是 <VLOOKUP>可以幫助將統計的數字自動填入,讀者可以花一些時間熟練,處理很多事情會方便許多,比如在上圖,透過 <VLOOKUP>可以自動從統計的表格找到在轉輪1~5裡 WK等等的統計資料,「出現次數」則是將每個轉輪的相應符號次數相乘,這裡的計算邏輯可以看上方 (2) 3 連線、4 連線、5 連線 的部分再複習一次。
3.算出現機率
將出現次數除以所有的可能數(每個滾輪的符號總數相乘)便是該得分組合的機率。
![图片[12]-老虎機數學入門 PART Ⅰ-学游戏](http://blog.ftuta.com/wp-content/uploads/2024/07/image-8-1024x268.png)
4.算期望值
還記得前面提的期望值吧!這時將機率乘以得分就得到囉。
![图片[13]-老虎機數學入門 PART Ⅰ-学游戏](http://blog.ftuta.com/wp-content/uploads/2024/07/image-9-1024x255.png)
接著再將所有得分組合的期望值相加,便可以得到總期望值
到此,原先感覺複雜的東西經過拆解,輕鬆算完,可以瀟灑收工囉!
来源:slot设计王















暂无评论内容