连线彩金-数学篇

这篇文章就来为各位揭开彩金机率背后的面纱。 （本篇的描述范例皆是以「多福多财」类型的连线彩金为例子）

首先要先了解的是

连线彩金的数学基础

1. 期望值RTP：连线彩金是游戏的一部份，不论玩家押分多少，都会占游戏中固定比例的RTP。
2. 彩金大小：连接同一组连线彩金的每台机器其彩金大小都是一样的，即使每台机器的玩家同时间押分大小不一定相同。
3. 中奖机率：彩金大小一样且押分大小不同的情况下，要维持固定的RTP ，必须让获得彩金的机率与押分大小成正比。

连线彩金的数学设定

• 每分机率 : 玩家押分的每一分值(cent) 获得彩金的机率，是一个固定值，符合上面3. 所描述押分越大中奖机率也越大，两者成正比。
• 滚动率(Increment)  : 玩家所有下注金额贡献到彩金池中的固定比例，这会让金额不断增加，同时也是连线彩金最大的卖点。
• 起始金额(Start-up)  : 每当有玩家获得彩金大奖后，奖金数字回到一个固定金额重新开始累计。

连线彩金的期望值计算

以单一奖项的彩金来说，只要设定好每分机率、滚动率以及起始金额这三项数值，我们就能算出该彩金的期望值。

连线彩金的期望值可以拆成

1. 起始金额期望值：由于起始彩池金额是固定的，以期望值的基本定义来计算可得：起始金额期望值= 起始金额x 每分机率
   
2. 滚动率期望值：滚动率的部分由于没有固定的彩池金额以及机率，我们需要从另一个角度思考，以最简单的情况来出发，我们假设现在只有一个玩家在玩这个连线彩金。在玩家获得彩金前玩家肯定是拿不到任何东西；但当玩家获得彩金时，在起始金额以外的部分玩家能拿到的就是「之前玩家所有押注金额里贡献到彩金池的部分」，也就是玩家所有押注金额x 滚动率。故彩金中起始金额以外的期望值就相当于滚动率：滚动率期望值= 滚动率

两项合并起来后我们有了连线彩金的期望值：连线彩金期望值= 起始金额x 每分机率+ 滚动率

多彩池连线彩金

现在单一彩金池的彩金我们会算了，但实际在赌场看得到的彩金是以多彩金池为主。相信有去过赌场的赌者们一定对 Grand、Major、Minor、Mini 等彩金池的名称有印象吧。现在就来看看如果是多个彩金池的彩金会有什么变化。

「多福多财」的多彩池连线彩金在触发彩金小游戏时，玩家会从4个不同等级的彩金中随机获得1个。

首先每个彩金池都会有各自的起始金额、滚动率，但只会有一个每分机率(也就是每一分值进入彩金小游戏的机率)，当进入彩金小游戏时每个彩金池又会有各自的中奖机率。

多彩池连线彩金的数学设定

• 每一分值(cent)进入彩金小游戏的机率：每分机率
• Grand：起始金额A、滚动率A、奖项机率A
• Major：起始金额B、滚动率B、奖项机率B
• Minor：起始金额C、滚动率C、奖项机率C
• Mini：起始金额D、滚动率D、奖项机率D

须注意的是奖项机率A~D加起来要是100%

多彩池连线彩金的期望值计算
四个彩金池的期望值可以独立拆开来处理

• Grand期望值 = 起始金额A x 奖项机率A x 每分机率+ 滚动率A
• Major期望值 = 起始金额B x 奖项机率B x 每分机率+ 滚动率B
• Minor期望值= 起始金额C x 奖项机率C x 每分机率+ 滚动率C
• Mini期望值 = 起始金额D x 奖项机率D x 每分机率+ 滚动率D

多彩池连线彩金期望值
= Grand期望值+ Major期望值+ Minor期望值+ Mini期望值
= ∑ _{( K = A to D )}  ( 起始金额_K x 奖项机率_K x 每分机率+ 滚动率_K )

来看个实际数字的例子：

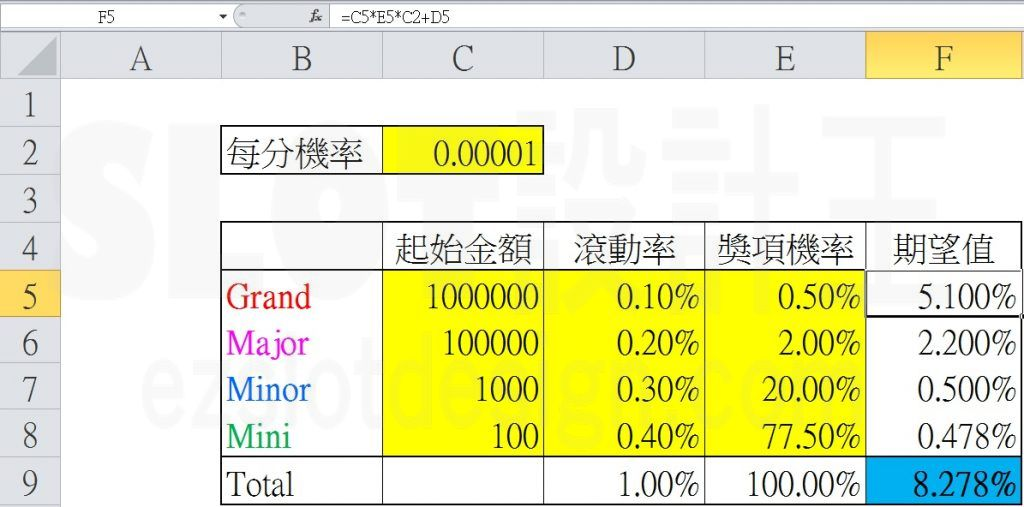
利用上面公式我们能计算出彩金的期望值(也就是图中蓝底储存格的8.278%)，接着调整每分机率或各彩金的起始金额、滚动率与中奖机率，使彩金期望值符合需求，如此一来就能完成一套符合需求期望值的彩金数学了。

来源：slot设计王